高中数学必修一《方程的根与函数的零点》教学设计
11-01 11:53:31 | 浏览次数: 42318 次 | 栏目:数学教学设计
标签:数学教学设计,http://www.manfen6.com
高中数学必修一《方程的根与函数的零点》教学设计,





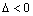



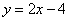
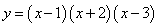




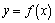

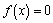
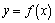

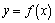
TAG: 教学 高中数学
,函数在区间上不单调;④
,函数在区间上单调,等各种情况,加深学生对零点存在性定理的理解.
四.教学支持条件分析
本节教学目标的实现,需要借助计算机或者计算器,一方面是绘制函数图象,通过观察图象加深方程的根、函数零点以及同时函数图象与
轴的交点的关系;另一方面,判断零点所在区间过程中,一些函数值的计算也必须借助计算机或计算器.
五.教学过程设计
1.方程的根与相应函数图象的关系
复习总结一元二次方程与相应函数与
轴的交点及其坐标的关系:
一元二次方程根的个数
图象与
轴交点个数
图象与
轴交点坐标
意图:回顾二次函数图象与
轴的交点和相应方程的根的关系,为一般函数及相应方程关系作准备.
问题一、上述结论对其他函数成立吗?为什么?
在《几何画板》下展示如下函数的图象:
、
、
、
、
,
比较函数图象与
轴的交点和相应方程的根的关系。
函数
的图象与
轴交点,即当
,该方程有几个根,
的图象与
轴就有几个交点,且方程的根就是交点的横坐标.
意图:通过各种函数,将结论推广到一般函数。
2.函数零点概念
对于函数
,把使
- ·上一篇:英语励志格言:知己方能解人
- ·下一篇:《就英法联军远征中国给巴特勒上尉的信》赏析
《高中数学必修一《方程的根与函数的零点》教学设计》相关文章
- › 高中数学集合与函数公式定理记忆口诀
- › 高中数学公式汇总
- › 高中数学三角函数公式定理记忆口诀
- › 了解高中数学特点是高一数学学习关键
- › 高中数学与初中数学有哪些变化
- › 高一同学必读:如何学好高中数学 ?
- › 北京四中名师指点:从高一开始学好高中数学
- › 高一新生篇:如何学好高中数学
- › 高中数学笔记误区分析
- › 高中数学学习方法指导
- › 影响高中数学成绩的原因及解决方法
- › 高中数学第一轮复习建议
- › 高中数学公式大全
- › 怎样学好高中数学-学好高中数学的几个技巧
- › 高中数学教学总结与反思
- › 浅谈影响高中数学成绩的原因
- 在百度中搜索相关文章:高中数学必修一《方程的根与函数的零点》教学设计
最新更新