高中数学《立体几何》单元测试

11-01 11:08:34 | 浏览次数: 42918 次 | 栏目：数学知识点总结

标签：数学知识点总结,http://www.manfen6.com 高中数学《立体几何》单元测试,

　　面面平行的思路，在平面B1D1H内寻找B1D1和O’H两条关键的相交直线，转化为证明：B1D1∥平面BDF，O’H∥平面BDF

　　⑶A1O⊥平面BDF，由三垂线定理，易得BD⊥A1O，再寻A1O垂直于平面BDF内的另一条直线。猜想A1O⊥OF。借助于正方体棱长及有关线段的关系计算得：A1O2+OF2=A1F2

　　A1O⊥OF。

　　⑷∵ CC1⊥平面AC∴ CC1⊥BD 又BD⊥AC∴ BD⊥平面AA1C 又BD

　　平面BDF

　　∴ 平面BDF⊥平面AA1C

　　18. 解析：

　　在平面ABC内作AE∥BC，从而得∠DAE=600

　　∴ DA与BC成600角

　　过B作BF∥AC，交EA延长线于F，则∠DBF为BD与AC所成的角

　　由△DAF易得AF=a，DA=a，∠DAF=1200∴ DF2=a2+a2-2a2·(

　　)=3a2　　∴ DF=

　　DBF中，BF=AC=

　　a∴ cos∠DBF=

　　∴ 异面直线BD与AC成角arccos

　　(3)∵ BA⊥平面ADE∴ 平面DAE⊥平面ABC

　　故取AE中点M，则有DM⊥平面ABC;取BC中点N，由MN⊥BC，根据三垂线定理，DN⊥BC

　　∴ DN是D到BC的距离　　　在△DMN中，DM=

　　a，MN=a∴ DN=

　　(4)∵ BF

　　平面BDF，AC

　　平面BDF，AC∥BF∴ AC∥平面BDF　　又BD

　　平面BDF

　　∴ AC与BD的距离即AC到平面BDF的距离∵

　　，

　　∴

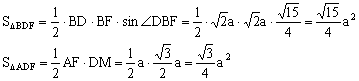
　　由

　　，即异面直线BD与AC的距离为

　　19. 解析：作AE⊥CD于E，BF⊥CD于F，则EF为异面直线AE、BF的公垂段，AE与BF成600角，可求得|AB|=

　　，当x=

　　时，|AB|有最小值