高一必修二《直线、平面、简单几何体》练习题
11-01 11:57:02 | 浏览次数: 83818 次 | 栏目：数学知识点总结
标签：数学知识点总结,http://www.manfen6.com
高一必修二《直线、平面、简单几何体》练习题,
TAG: 练习题 平面 几何体
⑶求二面角C-AB1-B的大小。
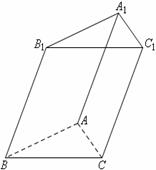
22..如图所示，AF、DE分别是⊙O、⊙O1的直径.AD与两圆所在的平面均垂直，AD=8,BC是⊙O的直径，AB=AC=6，OE//AD.
(Ⅰ)求二面角B—AD—F的大小;
(Ⅱ)求直线BD与EF所成的角.
参考答案
一、选择题
DAABC DDDCA BD
二、填空题
13.
14.③⑤ ②⑤ 15.
16.2/3
三、解答题
17.⑴取AB中点E，则显然有FD∥EC
DF∥平面ABC
⑵
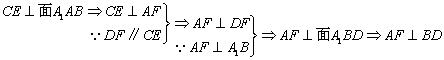
18.解法一：(Ⅰ)设O为AC中点，连结EO，BO，则EO
又CC1
B1B，
所以EO
DB ，则EOBD为平行四边形， ED∥OB
∵ AB = BC，∴ BO⊥AC ，又面ABC⊥面ACC1A1，BO
面ABC ，故BO⊥面ACC1A1
∴ ED⊥面ACC1A1，ED⊥AC1，ED⊥CC1 ∴ ED⊥BB1
ED为异面直线AC1与BB1的公垂线
(Ⅱ)联结A1E，由AA1 = AC =
AB可知，A1ACC1为正方形，
∴ A1E ⊥AC1 由ED⊥面A1ACC1和ED
面ADC1知面ADC1⊥面A1ACC1
ED⊥A1E
则A1E⊥面ADE。 过E向AD作垂线，垂足为F，连结A1F，
由三垂线定理知∠A1FE为二面角A1—AD—C1的平面角。
不妨设AA1 = 2 ，则AC = 2 ，AB =
， ED = OB = 1 ，
EF =
所以二面角A1—AD—C1为60°
19..解：(1) ∵BC∥B1C1, ∴∠ACB为异面直线B1C1与AC所成角(或它的补角)
∵∠ABC=90°, AB=BC=1, ∴∠ACB=45°, ∴异面直线B1C1与AC所成角为45°.
(2) ∵AA1⊥平面ABC,∠ACA1是A1C与平面ABC所成的角, ∠ACA =45°.
∵∠ABC=90°, AB=BC=1, AC=
,∴AA1=
.
20.⑴由三垂线定理可得，A1C⊥BD，A1C⊥BE
A1C⊥平面BDE
⑵以DA、DC、DD1分别为x、y、z轴，建立坐标系，则
- ·上一篇：八年下册暑假园地答案
- ·下一篇：七年级数学《直线、射线、线段》同步测试题
《高一必修二《直线、平面、简单几何体》练习题》相关文章
- › 高一必修二《两条直线的平行与垂直》练习题
- › 高一必修二《直线的方程》练习题
- › 关于高一生物复习方法：高一必修复习提纲
- › 荆轲刺秦王(人教版高一必修)
- › 人教版高一必修4文言文阅读同步训练
- › 人教版高一必修一英语教案
- › 高一必修二《直线与方程》课堂练习
- › 高一必修二《圆与方程》课堂练习
- › 高一必修二《直线、平面、简单几何体》练习题
- › 高一必修一《直线与平面垂直的判定(一)》教案
- › 高一必修二《点到直线的距离》说课稿
- › 高一必修二《圆的标准方程》的说课稿
- › 北师大版高一必修二数学教案
- › 北师大版高一必修三数学教案
- › 牛津英语高一必修一教案
- › 高一必修一《圆的方程》教学设计
- 在百度中搜索相关文章：高一必修二《直线、平面、简单几何体》练习题
最新更新