双曲线方程知识点总结
11-01 11:57:02 | 浏览次数: 58818 次 | 栏目:数学公式
标签:数学公式,http://www.manfen6.com
双曲线方程知识点总结,
,离心率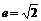 .
.
⑷共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线,叫做已知双曲线的共轭双曲线. 与
与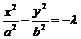 互为共轭双曲线,它们具有共同的渐近线:
互为共轭双曲线,它们具有共同的渐近线: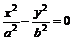 .
.
 ⑸共渐近线的双曲线系方程:
⑸共渐近线的双曲线系方程: 的渐近线方程为
的渐近线方程为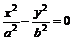 如果双曲线的渐近线为
如果双曲线的渐近线为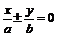 时,它的双曲线方程可设为
时,它的双曲线方程可设为 .
.
例如:若双曲线一条渐近线为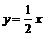 且过
且过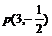 ,求双曲线的方程?
,求双曲线的方程?
解:令双曲线的方程为: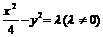 ,代入
,代入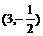 得
得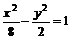 .
.
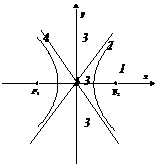
⑹直线与双曲线的位置关系:
区域①:无切线,2条与渐近线平行的直线,合计2条;
区域②:即定点在双曲线上,1条切线,2条与渐近线平行的直线,合计3条;
区域③:2条切线,2条与渐近线平行的直线,合计4条;
区域④:即定点在渐近线上且非原点,1条切线,1条与渐近线平行的直线,合计2条;
区域⑤:即过原点,无切线,无与渐近线平行的直线.
小结:过定点作直线与双曲线有且仅有一个交点,可以作出的直线数目可能有0、2、3、4条.
(2)若直线与双曲线一支有交点,交点为二个时,求确定直线的斜率可用代入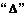 法与渐近线求交和两根之和与两根之积同号.
法与渐近线求交和两根之和与两根之积同号.
⑺若P在双曲线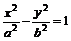 ,则常用结论1:P到焦点的距离为m = n,则P到两准线的距离比为m︰n.
,则常用结论1:P到焦点的距离为m = n,则P到两准线的距离比为m︰n.
简证: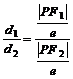 =
=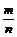 .
.
常用结论2:从双曲线一个焦点到另一条渐近线的距离等于b.
TAG: 知识点 双曲线
,离心率
⑷共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线,叫做已知双曲线的共轭双曲线.
 ⑸共渐近线的双曲线系方程:
⑸共渐近线的双曲线系方程:例如:若双曲线一条渐近线为
解:令双曲线的方程为:
⑹直线与双曲线的位置关系:
区域①:无切线,2条与渐近线平行的直线,合计2条;
区域②:即定点在双曲线上,1条切线,2条与渐近线平行的直线,合计3条;
区域③:2条切线,2条与渐近线平行的直线,合计4条;
区域④:即定点在渐近线上且非原点,1条切线,1条与渐近线平行的直线,合计2条;
区域⑤:即过原点,无切线,无与渐近线平行的直线.
小结:过定点作直线与双曲线有且仅有一个交点,可以作出的直线数目可能有0、2、3、4条.
(2)若直线与双曲线一支有交点,交点为二个时,求确定直线的斜率可用代入
⑺若P在双曲线
简证:
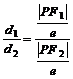 =
=常用结论2:从双曲线一个焦点到另一条渐近线的距离等于b.
- ·上一篇:四年级暑假数学作业答案2016
- ·下一篇:高中英语说课稿:《高中英语第二册第54课》优秀说课稿范例
《双曲线方程知识点总结》相关文章
- › 双曲线方程知识点总结
- 在百度中搜索相关文章:双曲线方程知识点总结
最新更新
- · 初中数学一元二次方程公式定理
- · 常见问题的公式(一)
- · 小学生数学公式大全:平行四边形
- · 小学生数学公式大全:长方形
- · 小学生数学公式大全:正方形
- · 圆周长的计算公式
- · 高中数学集合与函数公式定理记忆口诀
- · 小学数学公式大全
- · 加减乘除和差倍公式
- · 常见问题的公式(二)
- · 高中数学公式汇总
- · 常用数学公式表大全
- · 高中数学三角函数公式定理记忆口诀
- · 等比数列公式
- · 等差数列求和公式
- · 初中数学函数与图像公式定理
热门排行
- · 长方形的表面积公式
- · 初中数学有理数及其运算公式定理
- · 圆周长的计算公式
- · 平行四边形面积公式
- · 常见问题的公式(一)
- · 小学生数学公式大全:平行四边形
- · 小学数学反向行程问题公式
- · 圆的周长公式
- · 小升初数学复习资料:长度等的定义及常用单
- · 加减乘除和差倍公式
- · 球的表面积计算公式
- · 小学生数学公式大全:利率问题公式