高中数学必修一《函数的单调性》教学设计
11-01 11:08:11 | 浏览次数: 75418 次 | 栏目:数学教学设计
标签:数学教学设计,http://www.manfen6.com
高中数学必修一《函数的单调性》教学设计,
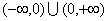
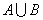
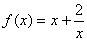
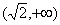
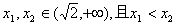
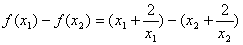
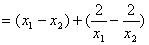

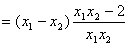
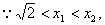
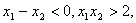
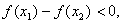
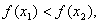
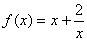
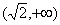
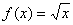
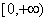
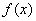
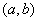
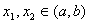
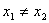
TAG: 教学 高中数学 单调性
在
上是减函数.
通过判断题,强调三点:
①单调性是对定义域内某个区间而言的,离开了定义域和相应区间就谈不上单调性.
②对于某个具体函数的单调区间,可以是整个定义域(如一次函数),可以是定义域内某个区间(如二次函数),也可以根本不单调(如常函数).
③函数在定义域内的两个区间A,B上都是增(或减)函数,一般不能认为函数在
上是增(或减)函数.
思考:如何说明一个函数在某个区间上不是单调函数?
〖设计意图〗让学生由特殊到一般,从具体到抽象归纳出单调性的定义,通过对判断题的辨析,加深学生对定义的理解,完成对概念的第三次认识.
三、掌握证法,适当延展
例 证明函数
在
上是增函数.
1.分析解决问题 针对学生可能出现的问题,组织学生讨论、交流.
证明:任取
, 设元
求差
变形
,
断号
∴
∴
即
∴函数
在
上是增函数. 定论
2.归纳解题步骤
引导学生归纳证明函数单调性的步骤:设元、作差、变形、断号、定论.
练习:证明函数
在
上是增函数.
问题:要证明函数
在区间
上是增函数,除了用定义来证,如果可以证得对任意的
,且
有
- ·上一篇:《匆匆》同步范文2 成长的烦恼
- ·下一篇:傅雷的艺术观和做人观
《高中数学必修一《函数的单调性》教学设计》相关文章
- › 高中数学集合与函数公式定理记忆口诀
- › 高中数学公式汇总
- › 高中数学三角函数公式定理记忆口诀
- › 了解高中数学特点是高一数学学习关键
- › 高中数学与初中数学有哪些变化
- › 高一同学必读:如何学好高中数学 ?
- › 北京四中名师指点:从高一开始学好高中数学
- › 高一新生篇:如何学好高中数学
- › 高中数学笔记误区分析
- › 高中数学学习方法指导
- › 影响高中数学成绩的原因及解决方法
- › 高中数学第一轮复习建议
- › 高中数学公式大全
- › 怎样学好高中数学-学好高中数学的几个技巧
- › 高中数学教学总结与反思
- › 浅谈影响高中数学成绩的原因
- 在百度中搜索相关文章:高中数学必修一《函数的单调性》教学设计
最新更新