七年级下册《多边形的内角和》教学案例

标签：数学教学设计,http://www.manfen6.com 七年级下册《多边形的内角和》教学案例,

 

　　的大小能确定。

　　变式：此题中

　　

 

　　的大小若能确定，试求

　　

 

　　的度数;若不能确定，请说明理由。

　　生口答：

　　

 

　　对于学生的回答教师及时给予肯定表扬。

　　点评 设计此组练习的目的一是使学生进一步理解四边形的内角和是

　　

 

　　的内涵和外延。二是教师可了解学生学习情况，以便及时的调整和改进教学。

　　(四)变式训练

　　师：请同学们看下面的题目。

　　已知：如图10，直线

　　

 

　　，垂足为B，直线

　　

 

　　，垂足为C，问

　　

 

　　与

　　

 

　　之间会有怎样的关系?对你的结论请给予说明。

　　

 

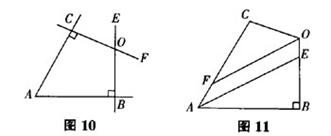
　　生思考──交流──说明问题的答案──互评。

　　师：请同学们继续思考，图中有与

　　

 

　　相等的角吗?若有请指出，并给出说明;若没有请说明理由。

　　学生继续交流、探讨。

　　师追问：我们将此题目增加条件，又构成了一道新的探索型问题。请同学们继续思考解答。

　　已知：如图11，在四边形ABOC中，

　　

 

　　，AE平分

　　

 

　　，OF平分

　　

 

　　，请问AE与OF平行吗?为什么?

　　学生交流、探讨。

　　点评 这是一组系列探索题。这个题目知识覆盖面大，综合性强，题意构思精巧。这迫使学生要用“动”的观点去分析已知条件和面临结论之间的关系，在矛盾冲突中建立新的知识结构。在这个过程中，不同层次的学生都得到不同程度的发展与提高，学生的思维又上了一个新层次。

　　(五)引申思考

　　师：在得到四边形内角和是

　　

 

　　的基础上，你能探求五边形、六边形和一般n边形的内角和是多少度吗?请同学们思考研究。

　　

 

　　师生共同回答：n边形的内角和为：

　　

 

　　师：看谁回答的最快。

　　(l)六边形的内角和是 ;12边形的内角和是 。

　　(2) 边形的内角和是

　　

 

　　;一个多边形的内角和是

　　

 

　　，则这个多边形的边数是 。

　　(3)正六边形的一个内角是 。

　　(六)归纳小结(教师引导学生从以下几个方面进行小结)

　　1、研究问题的一般思维方法：

　　观察、分析、猜想、类比、解释、说明、应用。

　　2、研究几何概念及性质的一般思维方向：

　　定义、定义的内涵和外延。

　　就四边形而言有：边、角、对角线、内角和(教师提示：以及后面学习的外角和)。

　　3、四边形内角和是

　　

上一页  [1] [2] [3] [4]  下一页

TAG: 教学